2 VORSCHAU UND TEST PROTON, NEUTRON
GERMAN ▶
VORSCHAU
Der Ansatz gehört in den Papierkorb, sollte es nicht gelingen, die Up- und Down-Oszis so zu bestimmen, dass sich Proton und Neutron ergeben. Dies ist nicht trivial, da mit dem Schalenmodell Massendefekte auftreten (klassische QM). Dabei zeigt sich eine arithmetische Symmetrie. Die ist verbunden mit einer Störung (±), die der Masse des Elektrons entspricht.
Kapitel TESTFALL PROTON, NEUTRON siehe weiter unten.
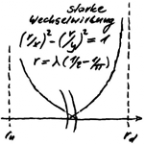
Kapitel STARKE WECHSELWIRKUNG UND SEPARATION.
Kapitel GRAVITATION UND NOETHER-THEOREM.
Die nachfolgenden Kapitel beschäftigen sich mit den Lösungen des sich ergebenden Variationsproblems. Dabei geht es um den existenziellen Nachweis der Leptonen (echte Quantentheorie).
letzte Änderung 01.03.2019
TESTFALL PROTON, NEUTRON
Erst wenn der Ansatz bei den Nukleonen nicht versagt, kann es weitergehen. Bis dahin geht um klassische Quantenmechanik. Da Proton und Neutron ein Schalenmodell aus Up- und Down-Oszis bilden, ist Folgendes zu testen:
- Stimmen Ladung und Spin? Und wenn ja, ist das Schalenmodell dann eineindeutig?
- Lassen sich die reduzierten Wellenlängen für das Up- und Down-Oszi so bestimmen, dass die Massen vom Proton und Neutron stimmen (die Durchmesser sind Zugabe)?
Up- und Down-Oszi sind primitive Oszis. Ladung und Spin ergeben sich somit durch Integration von E- bzw. B-Feld in Ausbreitungsrichtung, und zwar nach den Regeln der Schulmathematik. Die Amplitude wird auf ¼ festgesetzt, damit die Qunatenzahlen für die Ladung und Spin 1 wird. Spin 1 in der TO entspricht damit klassisch ½. Der Wert hat per Definition etwas mit dem g-Wert zu tun (1 bleibt 1, statt 2 mal ½). Bei der Dipolwelle ergeben Ladung und Spin 0. Hinter der Quantenzahl steht natürlich in der TO ein Vektor, deren Lage im Raum von der Symmetrie bestimmt wird. Auch beim Proton und Neutron ergeben sich die Quantenzahlen erst über eine vektorielle Zwischenrechnung. Die Up- und Down-Oszis werden entsprechen den Strukturformeln für das Proton bzw. Neutron ineinander geschachtelt. Der Aufbau des sich so ergebenden Schalenmodells wird erst mit dem Dilemma der QT eineindeutig.
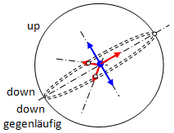
Achtung, in den Skizzen finden Sie nur die Pfeile, die sich wegheben: blau = Spin, rot = Ladung.
Proton: Ladung 1, Spin 1.
Die Kreisbahn des Down-Oszis ist völlig frei.Die Kreisbahnen der zwei Up-Oszis liegen in einer Ebene und sind gegenläufig.
Neutron: Ladung 0, Spin 1.Die Down-Oszis liegen in einer Ebene.Die Phasenverschiebung der Bahnen gegeneinander beträgt 120°.Das Up-Oszi kann nur um seine Ladungsachse drehen.
Es geht nun um die Bestimmung der reduzierten Wellenlänge λ vom Up- und Down-Oszi, und zwar so, dass sich die bekannten Massen vom Proton und Neutron ergeben. Damit ist zwar das Ergebnis bekannt, aber nicht der Lösungsweg, der in diesem Fall eindeutig sein muss. Dies erinnert an die Schulzeit, wenn trotz bekanntem Ergebnis überhaupt nicht klar war, was zu tun ist. Ein Blick ins Lehrbuch hilft da auch nicht, wenn nicht klar ist, wo zu suchen ist. Genau dies beschreibt die Situation. Mit den bekannten Strukturformeln vom Neutron (1Up + 2Down) und Proton (2Up + 1Down) läuft es auf die Lösung eines linearen Gleichungssystems hinaus. Mit dem obigen Schalenmodell treten jedoch Massendefekte auf, womit es unterbestimmt ist. Der β-Zerfall ist insofern hilfreich, da mit ihm die Aufteilung der Massendefekte eindeutig wird. Das rechnerisch richtige Ergebnis ergibt sich aber nur bei Einhaltung folgender Symmetrie:
md = ms + me und mu= ms - me, wobei ms die Masse der arithmetischen Symmetrie ist. Damit ist md - mu = 2me.
Der Index d steht für das Down-Oszi, u für das Up-Oszi und e für das Elektron. Die eigentliche Berechnung, die nicht trivial ist, finden Sie in der PDF. Entscheiden ist, zu verstehen, dass über das bekannte Ergebnis ein eindeutiger Lösungsweg gefunden wurde. Der bedingt die arithmetische Symmetrie, die damit Teil der Theorie ist! Darüber hinaus ist nur noch die Masse des Elektrons als Störung relevant, die netterweise experimentell recht genau bestimmt ist.
Abgesehen davon, dass untere Tabelle auf der oberen fußt, ist anhand der Massendefekte zu erkennen, dass das Neutron stabiler als das Proton ist. Dass die Wirklichkeit diese Aussage Lügen straft, liegt an der gestörten Impulsübertragung beim Proton: Die Up-Schalen sind gegenüber der Down-Schale frei drehbar.
Exkurs in die spezielle Realtivitätstheorie (SRT): Da die TO die gravitative Wechselwirkung mit einschließt, sollte die Lorentzinvarianz des primitiven Oszis nachgewiesen werden. Die ist gegeben, wenn seine Transformationen im Minkowskiraum Elemente der eigentlichen Lorentzgruppe SO(3,1) sind. Dazu reicht es, dass die Abbildungen ihrer Geometrie auf sich selbst zur Drehgruppe SO(3) gehören, was offensichtlich ist (Mathematik für Physiker).
letzte Änderung 24.02.2019