3 STARKE WECHSELWIRKUNG UND SEPARATION
GERMAN ▶
DER WAHRSCHEINLICHKEITSRAUM DER STARKEN WECHSELWIRKUNG
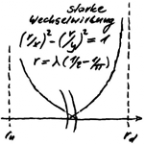
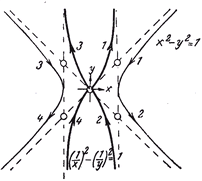
Das Schalenmodell macht die starke Wechselwirkung förmlich greifbar. Kreiswellen gleicher Wellenlänge verbinden sich zu sogenannten Oszi-Achten. Wäre die Acht ein Faden, so hat er eine maximale Streckung, bevor er definitiv reißt. Reißt, reißt nicht, womit nur zwei Ausgänge möglich sind. Mit dem Bernoulli-Experiment „Reißen der Oszi-Acht“, bleibt nur eine mögliche quadratintegrierbare Dichtefunktion y = f(x) übrig:
(1/x)² - (1/y)² = 1 mit x ϵ ]0, 1[, oder als Energiedichte
(r/x)² - (r/y)² = 1 mit x ϵ ]0, r[ und r = λ (1/2 + 1/π)
als Reichweite, wobei das Integral maximal r² ergibt.
Achtung, mit dem Dilemma der QT sind die Oszis als wahrscheinlichkeitstheoretisch unabhängig anzusehen, womit der allgemeine Multiplikationssatz gilt. Der erlaubt es erst, die richtigen Schlüsse zu ziehen. Auch wenn die Dichtefunktion aus einem Zufallsexperiment abgeleitet wurde, geht es hier um eine wohldefinierte Wahrscheinlichkeit: „Gott würfelt nicht!“ Up- und Down-Oszi sind schon sehr speziell:
Stehen Eu und Ed für die Energie der Kreiswellen, so ist mit ru und rd für die entsprechenden Reichweiten
Eu/rd = Ed/ru = 4,00971403630627 104 kgm/s² = v, mit v als Vertauschungsfaktor. Dann ist
Eu = v rd = v rd2/rd = Wd und analog Ed = v ru = v ru2/ru = Wu.
Das Vertauschungsphänomen ist gefunden. Es macht die Gluonen (Austauschteilchen) überflüssig! Schaltet man zwischen zwei Up-Oszis ein Down-Oszi wie im Proton, bzw. zwischen zwei Down-Oszis ein Up-Oszi wie im Neutron, so ergeben sich folgende Vertauschungssequenzen:
Proton Neutron
Eu – Wd|Ed – Wu Ed – Wu|Eu – Wd
Da beim direkten Austausch die Energien nicht passen, bleibt es bei 8 Vertauschungen. 8, da das Down-Oszi im Proton und das Up-Oszi im Neutron zweimal mit anderer Phasenverschiebung auftreten (habe mir die Indizierung gespart). Die Farbladungen sind damit überflüssig! Die starken WW hat das Dilemma der QT zu respektieren. Auf das Vertauschungsphänomen bezogen erlaubt dies den Schluss, dass seine Gültigkeit nicht ursächlich am Partner liegen kann. Zufall ist es aber auch nicht, wie sich später mit dem Kindergartenexperiment zeigen lässt - siehe NEUTRINOS ALS OSZIS UND MEHR.
Zur starken WW kommt es, wenn eine Ausbreitungslinie in den Bereich der Reichweite eindringt. Ihr Abstand bestimmt auf der Skala von 0 bis r = Reichweite die Obergrenze des Integrals über die Dichtefunktion. Da beim Zerreißen der Welle nur die Ausbreitungslinie interessiert, dürfen die Wellen zur Berechnung der starken WW in eine Ebene gedreht werden - der Vergißfunktor. Den Drehpunkt bestimmt die Punktsymmetrie. Die ergibt sich aus der geforderten Symmetrie des Oszis als Drahtmodell (Drehgruppe). Über die Punkte ergibt sich auch die gemeinsame Bezugslinie, auf der die Energiedichtefunktion aufzutragen ist. Die Null liegt auf dem Schnittpunkt mit der Ausbreitungslinie.
Bindungsparadoxon: Das Vertauschungsphänomen führt zu einem interessanten Ergebnis.
Da jeweils alle drei Oszi-Achten an der Bindung beteiligt sind, lassen sich folgende Energiegleichungen aufstellen:
Da jeweils alle drei Oszi-Achten an der Bindung beteiligt sind, lassen sich folgende Energiegleichungen aufstellen:
N≡N: 4Wd + 2Wu = 4Eu + 2Ed = 2 mal Kreiswellenenergie des Protons (2u + d)P≡P: 4Wu + 2Wd = 4Ed + 2Eu = 2 mal Kreiswellenenergie des Neutrons (2d + u)
Eine ausgeglichene Energiebilanz ergibt sich somit erst mit dem Heliumkern, womit sich sein Massendefekt jetzt überschlägig berechnen lässt. (siehe PDF, Anhang).
Als wahrscheinlichkeitstheoretischer Effekt kann die starke WW auftreten, oder nicht. Mit dem Dilemma der QT ist ihr wechselseitiges Auftreten bei zwei Wellen nur im Sinne von entweder-oder erlaubt. Andererseits sind die Wellen damit wahrscheinlichkeitstheoretisch unabhängig. Die Berechnung der resultierenden starken WW kann dann mit Hilfe des Multiplikationssatzes erfolgen. Mit dem Dilemma der QT kann also die starke Wechselwirkung nicht multitaskingfähig sein! Es gibt auch die starken WW einer Welle mit sich selbst. Bei der gefalteten Dipolwelle ist die starke WW = 0, denn Ober- und Untergrenze des Integrals sind = 0. Mit der Dichtefunktion lässt sich die Wahrscheinlichkeit auch wie folgt interpretieren: Ihre Gegenwahrscheinlichkeit ist ein Maß für das erneute Auftreten einer staken Wechselwirkung. Die Dipolwelle ist damit nur noch mit sich selbst beschäftigt. In Bezug auf die starke WW anderer Wellen ist sie quasi unsichtbar.
Der Raum der starken WW, also der speziellen quadratintegrierbaren Funktionen, ist ein Hilbertraum. Damit es sich um Quantentheorie handeln kann, darf es keine multiplikative Operation geben, die noch Element des Raumes, also kommutativ ist. Die Operation führt die starke WW hintereinander aus. Ausgehend von der arithmetischen Symmetrie Es und der Störung durch das Elektron ΔEs ergibt sich die geometrische Symmetrie
(Es + ΔEs)2 + (Es - ΔEs)2 = Ed2 + Eu2, bzw. Eu2 + Ed2 = 1, wobei der Unterstrich für die Normierung auf den Einheitskreis steht.
Mit dem Vertauschungsphänomen ergibt sich
Wd ◦ Wu = (Ed2 - Ed4)1/2 und Wu ◦ Wd = (Eu2 - Eu4)1/2.
Die Gleichungen zeigen, dass sich die starke WW des einen Oszis nicht auf die starke WW des anderen einlässt, womit der obige multiplikative Operator nicht kommutativ ist - was zu zeigen war.
Angeregtes Proton: Bei ihm zeigt ein Vergleich der klassischen Bewegungsgleichung mit der Integration über die Energiedichtefunktion, dass dies zu einer viel geringeren Auslenkung der Schwerpunkte führt, da die integrierten Werte weitaus stärker ansteigen. In der TO passt die Vorhersage zu den Ergebnissen des Experimentes, und die Seequarks sind überflüssig! Dass, was in das Standardmodell hinein gemogelt wurde, damit es passt, entfällt mit der TO. Ihre Effekte bleiben aber als mathematische Effekte erhalten!
Nullpunktsfluktuation: Ihre Existenz wird mit der Unschärferelation begründet. Die gilt aufgrund der Energiegleichung des Oszis jedoch nur innerhalb der Reichweite der starken WW, und da deren Energie aufgrund ihrer wahrscheinlichkeitstheoretischen Herleitung immer positiv ist, kann es in ihrem Gültigkeitsbereich keine Auslöschung, also auch keine Nullpunktsfluktuation geben!
letzte Änderung 24.02.2019
SEPARATION DER RÄUME
Der Raum sei der Raum, in dem die allgemeine Relativitätstheorie (kurz ART) gilt. Die elektromagnetische Feldtheorie (kurz EMF) beziehe sich auf diesen Raum. Sie selbst setzt als Raum das elektromagnetische Feld voraus. Die Beziehung ist jedoch zum Scheitern verurteilt, da die Zeit als vierte Dimension in ihnen unterschiedlich eingebunden ist. Die Unvereinbarkeit der Räume lässt sich jedoch mit Einsteins spezieller Relativitätstheorie (kurz SRT) abschwächen. Sie wird sowieso benötigt, und zwar von der Elektrodynamik. In der SRT lässt sich der Bezug der Zeit zu den restlichen Dimensionen recht einfach ausdrücken. In dieser Darstellung spricht man vom Minkowski-Raum. Mit ihm lässt sich zumindest lokal, also in jedem einzelnen Raumzeitpunkt die ART beschreiben.
Eine Separation von EMF und ART ist einerseits physikalisch notwendig, andererseits bleibt sie aber lokal unwirksam!
Die Lösung bringt die starke Wechselwirkung in Form des zugehörigen Wahrscheinlichkeitsraumes - siehe vorhergehendes Kapitel. Aufgrund seines wahrscheinlichkeitstheoretischen Charakters ist in ihm keine Zeit definiert! Andererseits sind wahrscheinlichkeitstheoretische Effekte als instantan anzusehen, womit sich der Raum bestens zur Separation der beiden Feldtheorien eignet. Da er in ihnen die Zeit synchronisiert, entsteht ein Sandwich. Dies hat nichts mit der immer wieder versuchten Vereinheitlichung zu tun! Die unterste Lage steht für die ART, die obere für die EMF, dazwischen liegt der wahrscheinlichkeitstheoretische Raum der starken Wechselwirkung, der das Sandwich nicht auseinanderfallen lässt. Abgesehen von der starken WW, erfolgt die Wechselwirkung über die entsprechende Feldtheorie. Folgendes ist damit zu beachten:
Jede Wechselwirkung wirkt sich auf den Raum als Ganzes aus, womit sie nicht isoliert betrachtet werden darf!
Ein Muss, denn ansonsten bliebe das Problem der Strahlungsrückkopplung ungelöst. Lösbar ist es bis heute nur in der Quantenelektrodynamik. Die Lösung erfordert aber die Quantenlogik und lässt die ART draußen. Sie einzubeziehen scheitert bekanntlich, solange die Maxwell-Gleichungen und die ART unangetastet bleiben. Da in der TO beide Theorien als gesichert angesehen werden, scheidet eine Vereinheitlichung von vornherein aus.
So etwas, wie eine Vereinheitlichung findet in der TO auch statt. Sie ergibt sich über die Lösung des Variationsproblems in der TO. Es wird sich nämlich im Laufe des Beitrags für jede Wechselwirkung eine spezielle Symmetrie ergeben. Zudem existiert eine allgemeine Symmetrie mit der einen Erhaltungsgröße, die allen Symmetrien gemeinsam ist. Es gilt also das Neother-Theorem. Die Symmetrien werden innerhalb des Variationsproblems durch Algorithmen beschrieben. Die sind aber nicht vom momentanen Zustand des Raumes abhängig, da sie sich nur noch auf die Invarianz unter der Wechselwirkung als Operation beziehen. Da Invarianz, Invarianz bleibt, kann dies auch wie folgt formuliert werden:
Eine Symmetrie, wie sie das Neother-Theorem erfordert, bleibt eine Symmetrie, egal wie sich die Raumzeit krümmt!
letzte Änderung 15.03.2019