7 SPOOKY PHOTON
ENGLISH ▶
The photon is a sine wave related to the E and B fields, but only of one period. As an open string it has two ends. The question is, what does their physical reality look like? First, two parallel photons of the same wavelength are to be investigated. From the chapter about neutrinos as oscis it can be deduced that their approach can never be total. According to the dilemma of QT, this behavior cannot be attributed to the photon as a quantum, but is owed to field theory. After the dilemma of the QT, annihilation cannot occur in any case.
So it just seems like there's zero point fluctuation. But after the TO they do not exist!
Polarisation: Simply changing the right angle between the E and B fields is not allowed after the QT dilemma, but the right angle refers to the unbent space-time. Polarization can also be generated with photons twisted against each other. After the last chapter, however, no mathematically correct rotary polarization can occur. This should be observable experimentally! Polarization and torsion of the wave in the gravitational field are to be distinguished. In the latter case, the wave appears rotated in the before-after comparison.
Shortest wavelength: It is determined in the TO by the minimum radius of curvature of the circular wave in the plane of the E field. The reason for this is that quantum processes cannot have a smaller wavelength.
With 5,876516699923 10-16 m as minimum radius is λ0 = 3,69232433863517 10-15 m,and thus E0 = h c/λ0 = 0,33578900862721 GeV (in the gamma radiation range).
The quantum number, which stands for the area integral of the sine wave, was determined arbitrarily. The area remains intact if the wavelength and amplitude are changed in inverse proportion. One more comment on the maximum energy of photons: Photons can link up. It is then a quantum object.
The behavior of the graph is more complex because the amplitude influences its length change. The reference figure is the extension factor λ'. It sets the length difference of graph and wavelength in relation to the wavelength, which should be in the counter of the quotient. Its function curve as a function of amplitude a is known:
If a < 1, their function value runs asymptotically against 0,25,if a > 1, it runs asymptotically against 0, which means that a = 1 is a turning point.Even if λ0' still increases with increasing wavelength,
remains λ0' under λ0' ‧ 1,16, because 0,25/0,216... = 1,15739... < 1,16.
The shortest wavelength is identified with a = 1, because then the extreme values lie on top of each other. If a were greater than 1, there would have to be an effect that can be associated with the turning point. This is not known. The arguments are admittedly weak, but perhaps a stronger argument will be found.
For the shortest wavelength λ0 = 3,69232433863517 10-15 m is then λ0' = 0,2160028025443.
The wavelength of the photon must remain constant in empty space. In the prestressed space-time continuum, this can only be ensured by limiting the oscillation space to the wavelength, which again results in the principle of constriction. The corresponding space-time line is constricted to the wavelength based on the length of the graph.
With wD = - 1,09020236896306 10-11 kgm/s2 as the energy density of the space-time line,
it is possible to for the photon with the shortest wavelength, establish the following energy equation:
E0 ART + E0 kin = wD λ0 λ0' + E0 kin = -8,69493521355215 10-27 kgm²/s² + E0 kin = 0,where E0 ART corresponds to a mass defect of -6,03829837739599 10-25 eV/c².
Even the longest wavelength photon thus remains below 1.16 times this value! The above equation must give 0 because the TO does not allow a negative energy balance (no zero fluctuation). So the photon is only massless at c - see also INTERPRETATION OF THE MASS. The first summand is the energy with which the photon counteracts its extension (holding the wavelength). With a higher negative energy density, this no longer works, which leads to a redshift. The above equation can also be interpreted differently. With the extension factor λ0' the photon is ironed (amplitude = 0). Thus, the photon once again confirms the conclusion that the universe has an event horizon. If, conversely, the rest mass were known, wD could be confirmed.
Gravitational and electromagnetic field theories show a relationship. This is reflected in the gravitational shift of the wavelength and the gravitational lens effect. Due to this relationship, it cannot be ruled out that they may have a resonant effect. The damping factors must be determined for this purpose. Since a photon remains photon as long as it is not absorbed, its electromagnetic damping is 0. A resonance catastrophe cannot occur with the dilemma of QT at the quantum level!
If the damping in the gravitational space were to be √½, the resonance increase would be 1. Thus the resonance amplitude would decrease exactly to the same extent as the effect of gravity. At stronger damping, gravity waves would not be detectable as forced swinging of astronomic events. In order not to have to think about a solution to Einstein's field equations, it is first a question of the prerequisite that leaves the constriction area unchanged. Its relativistic compression is of no interest. In any case, this requires that the divergence of the vector field at the ends of the constriction must remain 0 at certain points, because this is the only way to maintain the one-sided unsteadiness at the ends of the electromagnetic wave. Einstein's field equations allow this (conservation of energy and impulses).
If one considers the preservation of the constriction under the aspect of the resonance,
then the damping must be √½, because only in this way the divergence remains 0.
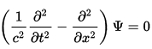
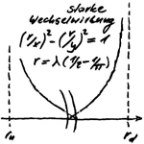
Divergence 0 affects the problem known as the classical borderline case of the harmonic oscillator. Classically interpreted, this results in a sharply defined oscillation. In quantum mechanics this becomes the wave equation (see right). The wave oscillates beyond the boundary, which can no longer correspond to quantum reality with the TO. Combined, the above dampings lead to resonance in the one room of the TO, which is actually a sandwich of rooms - see SEPARATION OF ROOMS. This explains the spooky distant effect of the photon. Since the oscillation propagates gravitatively with c, the oscillation is at the latest there, where the photon is, which reminds of the fairy tale "The rabbit and the hedgehog".
Quantum entanglement turns out to be a resonance event, and the ERP paradox is no longer one!
last modification 24.02.2019