8 INTERPRETATION DER MASSE

GERMAN ▶

Masse entsteht durch das „Prinzip der Einschnürung” augrund der ART. Oszis schnüren das Raum-Zeit-Kontinuum in der Ebene der Kreiswelle und in der Verlängerung der Dipolwelle als Achse ein. Einschnürung kann auch bedeuten, den Gürtel etwas zu lösen, wie bei den Neutrinos und Photonen. Es soll nun konkretisiert werden, wie Masse in diesem Kontext zu interpretieren ist. Dabei tritt die Schwierigkeit auf, dass die Einsteinschen Feldgleichungen auf ein viel zu komplexes System von Differentialgleichungen führen. Ihre heuristische Begründung legt aber eine Simulation nahe, in der Beschleunigung als schwarz-weiß schattiertes Bild im 3D-Raum sichtbar wird, und zwar über den Vorher-Nachher-Vergleich. In einfachen Fällen dürfte dies lokal eine numerische Lösung ermöglichen (Kontinuumsmechanik).

Zunächst soll es um die Teilchen gehen, die den Raum echt einschnüren. Wie schnell die Zeit in einem Punkt des Raumes vergeht, hängt von der dort herschenden Energiedichte ab. Da sich mit der TO eine universell gültige Energiedichte w00 für das leere Universum ergibt, gibt in ihr es auch eine universelle Geschwindigkeit, mit der die Zeit im leeren Universum verstreicht. Da die Geschwindigkeit, mit der die Zeit verstreicht, nur im Verhältnis zu dieser universellen Geschwindigkeit interessiert, wird der Quotient gebildet. Die universelle Geschwindigkeit gehört in den Nenner, denn nur so lassen sich unbestimmte Ausdrücke vermeiden. Zudem läuft so der Quotient proportional zur Energiedichte.

Bei w₀₀ ist der Quotient 1, was zum Beispiel einer Pigmentierung von 50% entsprechen könnte (Ausgangsfarbe voll schwarz = 100%). Ist die |Energiedichte| = 0, so steht die Zeit = schwarz. Bezogen auf die Einschnürung der Kreiswelle im Oszi vergeht die Zeit

im Innern schneller = heller, da dort die |Energiedichte| < |w₀₀| ist.

Entsprechendes gilt auch für die Dipolwelle. Um sich vom Drahtmodell des Oszis zu lösen, kann von einer einhüllenden Oberfläche ausgegangen werden, die sein Inneres vom Äußeren trennt (die Energiedichte hat dort ihren Wendepunkt). Das Oszi verteilt also die Pigmente um, was Arbeit erfordert.

Eine Umverteilung, die sich bei einer bestimmten Geschwindigkeit eingestellt hat, ändert sich so lange nicht, wie die Bewegung gleichförmig bleibt (mitziehen). Auf Beschleunigung reagiert das einzelne Pigment abhängig davon, wie schnell in dem Raumpunkt die Zeit vergeht. Die Geschwindigkeit ist and der Pigmentdichte in seiner direkten Umgebung abzulesen. Dies führt zu einer Verzerrung, die das Bild kontrastreicher erscheinen lässt. Die daraus resultierende Umverteilung der Pixel entspricht dem Zuwachs an kinetischer Energie.

Das einzelne Pigment folgt dabei im Modell Schwarzraum immer noch der Raumkrümmung, aber jetzt in einer 3-dimensionalen Simulation, deren Geschwindigkeit als Film allein durch die Rechenzeit begrenzt ist. Die Bewegung der Pigmente ist in diesem Modell grundsätzlich relativistisch zu betrachten. Ziel der Simulation ist es, die Lösung der Einsteinschen Feldgleichungen numerisch zu umgehen. Da der klassische Grenzfall des harmonischen Oszillators in der TO kein Problem mehr darstellt, lässt sich das Modell des Schwarzraumes auch auf makroskopische Objekte übertragen.

Alle Probleme, die sich mit dem Begriff Masse verbinden, scheinen sich nun mit dem Prinzip der Einschnürung erledigt zu haben. Nicht ganz, denn das Photon und die Neutrinos sind diesbezüglich speziell. Sie ziehen den vorgespannten Raum (negative Energiedichte) nicht zusammen, sondern entlasten ihn lokal, was zu einer negativen Energiebilanz führt, die es aber mit der TO nicht geben kann. Zum Schluss bleibt oft nur noch die kinetische Energie, um dies zu kompensieren. Der bis zu 0 fehlende Energiebetrag ist der Massendefekt, der mit der Erhöhung der Geschwindigkeit aber immer kleiner wird. Die so erzwungene Konvergenz lässt bei fehlender Nullpunktsfluktuation nur noch c als Grenzwert zu.

Neutrinos und Photonen sind somit erst bei c masselos!

Mit dem "Modell Schwarzraum" wird deutlich, dass obigen Argumentation schlüssig ist. Beim Neutrino und Photon ist im Schwarzraum die Verteilung der Pigmente entgegengesetzt zu den Teilchen, bei denen es um eine echte Einschnürung des Raumes geht. Sie sind innen dunkler als der Raum an sich. In diesem Fall verschwinden diese Helligkeitsunterschiede unter Beschleunigung immer mehr. Die Verteilung der Pigmente im Raum ist nun gleichmäßiger, womit seine Entropie gering ist. Da sie, wenn sie nicht zunimmt, nur noch gleich bleiben kann, ist sie in diesem Fall minimal. Die Minimierung der Entropie und die Minimierung der Gesamtenergie eines physikalisch abgeschlossenen Systems bedingen sich folglich. Dabei sagt die Entropie aber etwas darüber aus, wie gut die Minimierung bestenfalls gelingt. Entropie ist somit ein Maß für die Qualität des Raumzeitkontinuums!

Mit dem "Prinzip der Einschnürung" hat die Ansammlung von Materie einen Einfluss auf die Geschwindigkeit, mit der die Zeit in diesem Bereich vergeht. In Abhängigkeit von ihrer Struktur kann sie schneller oder langsamer vergehen. Die Ungereimtheiten, die in der klassischen Physik beim Brechungsindex und Casimir-Effekt auftreten, gibt es damit nicht mehr! Dabei ist zu beachten, dass sich dies auf den Raum zwischen den Elementarteilchen als Oszis bezieht.

Ein Exkurs in die SRT:

In ihr gilt folgende Beziehung zwischen Impuls und Energie.

p² c² + m² c⁴ = E² mit p = m v (1 - v²/c²)^-1/2
Wiederholt man in der TO das Stoßexperiment (Rechenweg siehe PDF zur TO), so ist
E_kin = E - m c² = m c² (1 - v²/c²)^-1/2 - m c²= m c² ((1 - v²/c²)^-1/2 - 1)
Allen Spekulationen, die sich an die Doppeldeutigkeit der Wurzel knüpfen, muss damit physikalisch eine Absage erteilt werden!

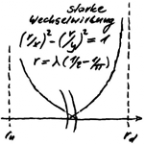
Neben dem didaktischen Problem mit der Masse gibt es noch das Problem mit den 4 physikalischen Grundkräften. In der TO gibt es nur noch drei, denn die schwache Kernkraft geht von den Wechselwirkungen der Dipolwelle aus. Das Wort Grundkraft impliziert, dass deren Herkunft nicht verstanden ist, was aber mit der TO nicht mehr der Fall ist. Eine Grundkraft ist an die entsprechende Wechselwirkung gebunden. Die findet im Raum der entsprechenden Feldtheorie statt. Eine Ausnahme bildet die starke Wechselwirkung, die wahrscheinlichkeitstheoretisch begründet ist. Der Raum ist ein spezieller Hilbertraum, der die Theorie erst zur Quantentheorie macht. Damit hat die naive Vorstellung von Grundkräften keinen Platz mehr in der TO!

letzte Änderung 25.05.2019

gehe zur Seite ◀ 0 1 2 3 4 5 6 7 8 9 ▶