3 STRONG INTERACTION AND SEPARATION
ENGLISH ▶
THE PROBABILITY SPACE OF STRONG INTERACTION
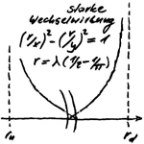
The shell model makes the strong interaction tangible. Circular waves of the same wavelength combine to form so-called osci-eights. If the figure eight were a thread, it would have a maximum elongation before it definitely breaks. Tears, does not tear, so that only two outputs are possible. With the Bernoulli experiment "Tearing the osci-eight", only one possible square-integratable density function y = f(x) remains:
(1/x)² - (1/y)² = 1 mit x ϵ ]0, 1[, or as energy density
(r/x)² - (r/y)² = 1 mit x ϵ ]0, r[ und r = λ (1/2 + 1/π)as the range, where the integral gives a maximum of r².
Attention, with the dilemma of the QT the oscillis are to be regarded as probabilistically independent, with which the general multiplication theorem applies. This allows the correct conclusions to be drawn first. Even if the density function was derived from a random experiment, this is a well-defined probability: "God does not roll!" Up- and down-osci are already very special:
If Eu and Ed stand for the energy of the circular waves, then ru and rd stand for corresponding ranges.Eu/rd = Ed/ru = 4,00971403630627 104 kgm/s² = v, with v as the permutation factor. Then
Eu = v rd = v rd2/rd = Wd and analog Ed = v ru = v ru2/ru = Wu.
The permutations phenomenon has been found. It makes the gluons superfluous! If one switches between two up-oscis a down-osci as in the proton, or between two down-oscis an up-osci as in the neutron, then the following exchange sequences result:
proton neutron
Eu – Wd|Ed – Wu Ed – Wu|Eu – Wd
Since the energies do not fit with the direct exchange, it remains with 8 exchanges. 8, because the down-osci in the proton and the up-osci in the neutron occur twice with a different phase shift (I was spared the indexing). The colour charges are therefore superfluous! The strong interaction has to respect the dilemma of the QT. With regard to the permutation phenomenon this allows the conclusion that its validity cannot be caused by the partner. But it is also not a coincidence, as can be shown later with the preschool experiment - see NEUTRINOS AS OSCIS AND MORE.
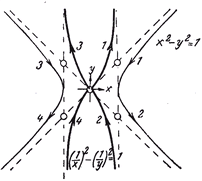
The strong interaction occurs when a propagation line penetrates into the range of the range. Their distance on the scale from 0 to r = range determines the upper limit of the integral via the density function. Since only the propagation line is of interest when the wave is torn apart, the waves may be rotated into one plane to calculate the strong interaction - the forget-funktor. The pivot point is determined by the point symmetry. This results from the required symmetry of the oscillation as a wire model (rotation group). The points also give the common reference line on which the energy density function is to be plotted. The zero lies at the intersection with the propagation line.
Bonding paradox: The permutation phenomenon leads to an interesting result.
Since all three oszi-eights are involved in the bond, the following energy equations can be established: folgende Energiegleichungen aufstellen:
N≡N: 4Wd + 2Wu = 4Eu + 2Ed = 2 times circular wave of the proton (2u + d)P≡P: 4Wu + 2Wd = 4Ed + 2Eu = 2 times circular wave of the neutron (2d + u)
A balanced energy balance is therefore only achieved with the helium nucleus, with which its mass defect can now be roughly calculated (see PDF, Anhang A.1).
The strong interaction may or may not occur as a probability-theoretical effect. With the dilemma of QT, its reciprocal occurrence in two waves is only allowed in the sense of either-or. On the other hand, the waves are thus independent in terms of probability theory. The resulting strong interaction can then be calculated using the multiplication theorem. With the dilemma of QT, the strong interaction cannot be a multitasking one! There is also the strong interaction of a wave with itself. With the folded dipole wave, the strong interaction is = 0, because the upper and lower limits of the integral are = 0. With the density function, the probability can also be interpreted as follows: Their contra-probability is a measure of the recurrence of a strong interaction. The dipole wave is only busy with itself. With regard to the strong interaction of other waves, it is virtually invisible.
The space of strong interaction, i.e. the special square-integratable functions, is a Hilbert space. For it to be a quantum theory, there must be no multiplicative operation that is still an element of space, i.e. commutative is. The operation executes the strong interaction one after the other. The operation performs the strong interaction one after the other. Starting from the arithmetic symmetry Es and the disturbance by the electron ΔEs the geometric symmetry results
(Es + ΔEs)2 + (Es - ΔEs)2 = Ed2 + Eu2, bzw. Eu2 + Ed2 = 1, where the underscore stands for the normalization to the unit circle.
The permutation phenomenon results in
Wd ◦ Wu = (Ed2 - Ed4)1/2 und Wu ◦ Wd = (Eu2 - Eu4)1/2.
The equations show that the strong interaction of one oscillation does not interfere with the strong interaction of the other, so that the above multiplicative operator is not commutative - which was to be shown.
Excited proton: A comparison of the classical equation of motion with the integration via the energy density function shows that this leads to a much lower deflection of the centers of gravity, since the integrated values increase much more strongly. In the TO, the prediction matches the results of the experiment, and the sea quarks are superfluous! The fact that what was cheated into the standard model to make it fit is not necessary with the TO. But their effects remain as mathematical effects!
Zero-point-energy: Their existence is based on the uncertainty principle. However, due to the energy equation of the oscillation, this only applies within the range of the strong interaction, and since its energy is always positive due to its probability-theoretical derivation, there can be no extinction, i.e. no zero point fluctuation, within its range of validity!
last modification 24.02.2019
SEPARATION OF ROOMS
Space is the space in which the general theory of relativity (GR for short) applies. The electromagnetic field theory (EMF for short) refers to this space. It itself presupposes the electromagnetic field as space. However, the relationship is doomed to failure, since time as the fourth dimension is differently integrated in them. However, the incompatibility of the spaces can be mitigated with Einstein's special theory of relativity (SR for short). It's needed anyway, in electrodynamics. In the SR, the relation of time to the other dimensions can be expressed quite simply. In this representation one speaks of the Minkowski room. With it the RT can be described at least locally, i.e. in each individual spacetime point.
A separation of EMF and RT is on the one hand physically necessary, on the other hand it remains locally ineffective!
The solution brings the strong interaction in the form of the associated probability space - see previous chapter.
Due to his probabilistic character, no time is defined in him! On the other hand, probability-theoretical effects are to be regarded as instantaneous, so that space is best suited for the separation of the two field theories. Since it synchronizes the time in them, a sandwich is created. This has nothing to do with the standardization which is tried again and again! The lowest layer stands for the RT, the upper layer for the EMF, in between lies the probability theoretical space of the strong interaction, which prevents the sandwich from falling apart. Apart from the strong interaction, the interaction takes place via the corresponding field theory. The following has to be considered:
Each interaction has an effect on the space as a whole, so it must not be viewed in isolation!
A must, because otherwise the problem of radiation feedback would remain unsolved. To this day, it can only be solved in quantum electrodynamics. The solution, however, requires quantum logic and leaves the GR outside. It is well known that their inclusion fails as long as the Maxwell equations and the ART remain untouched. Since in the TO both theories are regarded as secured, standardization is ruled out from the outset.
Something like standardization also takes place in the TO. It results from the solution of the variation problem in the TO. In the course of the contribution, a special symmetry will arise for each interaction. In addition, there is a general symmetry with the one constant that is common to all symmetries. So the Neother theorem applies. The symmetries are described within the variation problem by algorithms. However, they are not dependent on the momentary state of space, since they only refer to the invariance under the interaction as an operation. Since invariance, invariance remains, this can also be formulated as follows:
A symmetry, as required by the Neother theorem, remains a symmetry, no matter how space-time is curved!
last modification 15.03.2019