7 SPOOKY PHOTON
GERMAN ▶
Das Photon ist bezogen auf das E- und B-Feld eine Sinuswelle, aber nur von einer Periode. Als offener String besitzt es zwei Enden. Die Frage ist, wie sieht deren physikalische Realität aus. Zunächst soll es um zwei parallel laufende Photonen gleicher Wellenlänge gehen. Aus dem Kapitel über die Neutrinos als Oszis ist abzuleiten, dass ihre Annäherung nie total sein kann. Dies Verhalten kann nach dem Dilemma der QT nicht dem Photon als Quant zugeschrieben werden, sondern es ist der Feldtheorie geschuldet. Zur Annihilation kann es nach dem Dilemma der QT in keinem Fall kommen.
Damit scheint es nur so, als gäbe es Nullpunktfluktuation. Nach der TO gibt es sie jedoch nicht!
Polarisation: Einfach den rechten Winkel zwischen E- und B-Feld zu verändern, ist nach dem Dilemma der QT nicht erlaubt, wobei sich der rechte Winkel jedoch auf den nicht gekrümmten Raumzeit bezieht. Polarisation lässt sich auch mit gegeneinander verdrehten Photonen erzeugen. Nach dem letzten Kapitel kann aber keine mathematisch korrekte Drehpolarisation entstehen. Dies müsste eigentlich experimentel zu beobachten sein! Polarisation und Torsion der Welle im Gravitationsfeld sind zu unterscheiden. In letzten Fall erscheint die Welle beim Vorher-Nachher-Vergleich gedreht.
Kürzeste Wellenlänge: Sie ergibt sich in der TO über den minimalen Krümmungsradius der Kreiswelle in der Ebene des E-Feldes. Begründen lässt sich dies damit, dass bei Quantenprozessen keine kleinere Wellenlänge auftreten kann.
Mit 5,876516699923 10-16 m als minimalsten Radius ist λ0 = 3,69232433863517 10-15 m,und damit E0 = h c/λ0 = 0,33578900862721 GeV (liegt im Bereich der Gammastrahlung).
Die Quantenzahl, die für das Flächenintegral der Sinuswelle steht, wurde willkürlich festgelegte. Die Fläche bleibt erhalten, wenn Wellenlänge und Amplitude umgekehrt proportional abgeändert werden. Noch eine Anmerkung zur größtmöglichen Energie von Photonen. Photonen können sich verketten. Es handelt sich dann um ein Quantenobjekt.
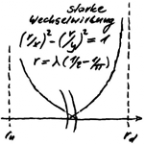
Das Verhalten des Graphen ist komplexer, da die Amplitude seine Längenänderung beeinflusst. Die Bezugsgröße sei der Verlängerungsfaktor λ'. Er setzt die Längendifferenz von Graph und Wellenlänge ins Verhältnis zur Wellenlänge, die im Zähler des Quotienten stehen soll. Sein Funktionsverlauf in Abhängigkeit von der Amplitude a ist bekannt:
Ist a < 1, so läuft ihr Funktionswert asymptotisch gegen 0,25,ist a > 1, so läuft er asymptotisch gegen 0, womit bei a = 1 ein Wendepunkt liegt.Auch wenn λ0' mit zunehmender Wellenlänge noch steigt,
bleibt λ0' unter λ0' ‧ 1,16, denn 0,25/0,216... = 1,15739... < 1,16.
Die kürzesten Wellenlänge wird mit a = 1 identifizieren, denn dann liegen die Extremalwerte aufeinander. Wäre a größer 1, so müsste es ein Effekt existieren, der sich in Verbindung mit dem Wendepunkt bringen lässt. Der ist nicht bekannt. Die Argumente sind zugegebenermaßen schwach, aber vielleicht wird noch ein stärkeres Argument gefunden.
Für die kürzeste Wellenlänge λ0 = 3,69232433863517 10-15 m ist dann λ0' = 0,2160028025443.
Die Wellenlänge des Photons muss im leeren Raum konstant bleiben. Im vorgespannten Raum-Zeit-Kontinuum ist dies nur dadurch zu gewährleisten, dass der Schwingungsraum auf die Wellenlänge begrenzt bleibt, was wieder auf das Prinzip der Einschnürung hinausläuft. Dabei wird die entsprechende Raumzeitlinie ausgehend von der Länge des Graphen auf die Wellenlänge eingeschnürt.
Mit wD = - 1,09020236896306 10-11 kgm/s2 als Energiedichte der Raumzeitlinie lässt sichfür das Photon mit der kürzesten Wellenlänge folgende Energiegleichung aufstellen:
E0 ART + E0 kin = wD λ0 λ0' + E0 kin = -8,69493521355215 10-27 kgm²/s² + E0 kin = 0,womit E0 ART einem Massendefekt von -6,03829837739599 10-25 eV/c² entspricht.
Selbst dass langwelligste Photon bleibt damit unter dem 1,16-Fachen dieses Wertes! Die obige Gleichung muss 0 ergeben, denn die TO lässt keine negative Energiebilanz zu (keine Nullpunktsfluktuation). Das Photon ist also erst bei c masselos - siehe auch INTERPRETATION DER MASSE. Der erste Summand ist die Energie, mit der das Photon seiner Verlängerung entgegenwirkt (halten der Wellenlänge). Bei größerer negativer Energiedichte klappt dies nicht mehr, was zur Rotverschiebung führt. Die obige Gleichung lässt sich auch anders interpretieren. Mit dem Verlängerungsfaktor λ0' ist das Photon gebügelt (Amplitude = 0). So betrachtet bestätigt das Photon noch einmal den Schluss, dass das Universum einen Ereignishorizont aufweist. Wäre umgekehrt die Ruhemasse bekannt, so ließe sich wD bestätigen.
Gravitative und elektromagnetische Feldtheorien zeigen einen Zusammenhang. Der zeigt sich in der gravitativen Verschiebung der Wellenlänge und dem gravitativen Linseneffekt. Aufgrund dieses Zusammenhangs kann nicht ausgeschlossen werden, dass sie in Resonanz treten können. Dazu sind die Dämpfungsfaktoren zu ermitteln. Da ein Photon, solange es nicht absorbiert wird, Photon bleibt, ist seine elektromagnetische Dämpfung 0. Eine Resonanzkatastrophe kann mit dem Dilemma der QT auf Quantenebene nicht eintreten!
Betrüge die Dämpfung im Gravitationsraum √½, so wäre die Resonanzerhöhung 1. Damit würde die Resonanzamplitude genau in dem Maße abnehmen, wie die Wirkung der Gravitation. Bei größerer Dämpfung wären die Gravitationswellen als erzwungene Schwingung astronomischer Ereignisse nicht nachweisbar. Um nicht über eine Lösung der Einsteinschen Feldgleichungen nachdenken zu müssen, soll es zunächst um die Voraussetzung gehen, die den Einschnürungsbereich unverändert lässt. Seine relativistische Stauchung interessiert dabei nicht. In jedem Fall verlangt dies, dass an den Enden der Einschnürung die Divergenz des Vektorfeldes punktuell 0 bleiben muss, denn nur so ist die einseitige Unstetigkeit an den Enden der elektromagnetischen Welle zu erhalten. Die Einsteinschen Feldgleichungen erlauben dies (Energie- und Impulserhaltung).
Betrachtet man den Erhalt der Einschnürung unter dem Aspekt der Resonanz,
so muss die Dämpfung √½ sein, denn nur so bleibt die Divergenz 0.
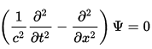
Die Divergenz 0 hat Auswirkungen auf das Problem, das als klassischer Grenzfall des harmonischen Oszillators bekannt ist. Klassisch interpretiert ergibt dies eine scharf abgegrenzte Schwingung. In der Quantenmechanik wird daraus die Wellengleichung (siehe rechts). Die Welle schwingt über die Abgrenzung hinaus, was mit der TO nicht mehr der Quantenrealität entsprechen kann. Kombiniert führen die obigen Dämpfungen zur Resonanz, und zwar in dem einen Raum der TO, der eigentlich ein Sandwich aus Räumen ist - siehe SEPARATION DER RÄUME. Dies erklärt die spukhafte Fernwirkung des Photons. Da sich die Schwingung gravitativ mit c ausbreitet, ist die Schwingung spätestens da, wo das Photon ist, was an das Märchen „Der Hase und der Igel“ erinnert.
Quantenverschränkung entpuppt sich als Resonanzereignis, und das ERP-Paradoxon ist keines mehr!
letzte Änderung 24.02.2019