4 GRAVITATION AND NOETHER'S THEOREM

ENGLISH ▶

GRAVITATIONAL INTERACTION

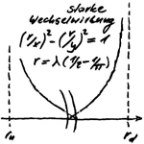
The idea for its calculation arises with the curtain on the window. If several folds are gathered by means of a loop, their constriction leads to a counter-reaction, which can be equated with gravity (negative). The folds of the curtain pre-defined by the pleating tape correspond to the scaling of the gravitational space. It is remembered that the perturbation of the pair of up- and down-osci ± one electron mass was found, with which the scaling of the gravitational space is found - called e-continuum for short.

Based on the up- and down-osci and their Compton-wavelength
λ_u = 3,96741355771958 10^-15 m and λ_d = 3,95448111261022 10^-15 m
the following diameters result as a circular shaft
d_u = 1,66484999566855 10^-15 m und d_d = 1,65942313989184 10^-15 m.
This allows you to calculate the scaling factor w0 that matches m_e:
w0 = ¼ (d_u - d_d) = 1,35671394417761 10^-18 m

For the 0-radius this results in

The gravitational symmetry of up- and down-osci is thus found.

With gravitational symmetry, the arithmetic mass of symmetry determined initially on the basis of the β-decay is correct, which had to be proven! Gravity is thus produced by the principle of constriction in the spacetime continuum. The principle has general validity. Attention, the absence of a spin component in Einstein's field equations with the TO is not a mistake, but a must! Starting from the pair of up- and down-osci the gravitative symmetry can be generalized. For a pair of oszis that satisfies the general symmetry, the following then applies

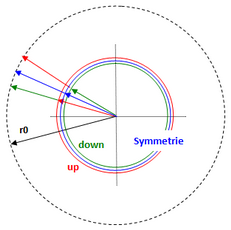
E_ges/w = r0 = r₁ + r₂, where r₁ = E₂/w und r₂ = E₁/w is.

This symmetry shows circular and dipole waves! With respect to the resulting variation problem, this means that the energy density is a local quantity. The path to the universally valid energy density of the quantum vacuum is later shown by the upward oscillation of the neutrino-oscis.

last modification 24.02.2019

GENERALIZATION AND NOETHER'S THEOREM

The Noether theorem (NT for short) states that every continuous symmetry leads to a conservation value, whereby the symmetry is equivalent to the "invariance under an operation". This is his most universal formulation. If it does not fit, none fits. In this case, the NT would have to apply equally to all three interactions, with a conserved quantity.

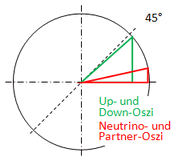
The conjunctive used above can be omitted for pairs of primitive oszis that satisfy the general symmetry. The pair of up- and down-oszi is the only solution to the associated variation problem. This can be recognized immediately when all relationships resulting from the symmetries recognized so far are compiled in a spreadsheet. Arithmetic symmetry, i.e. the perturbation by plus/minus an electron mass, naturally only occurs with the pair of up- and down osci, the solution. With geometric symmetry, which is to be called general symmetry from now on, the theorem of Pythagoras applies. If the symmetry energy is normalized to 1, this can be represented in the unit circle. The symmetry energy respectively the radius 1 is the conserved quantity in NT.

The variation problem is now to be generalized so far that the solutions include the leptons. For this purpose, the winding type of one of the osci's is unlocked. If the varastion problem remains solvable, it may only refer to a specific winding type. Despite this case distinction, there are more possibilities for geometric variation than in the case of the primitive osci. The possibilities must be restricted to such an extent that the NT remains valid. This presupposes that the symmetries continue to apply. Where this is not directly apparent, the "invariance under the corresponding operation", i.e. under the corresponding interaction, can fall back on.

If you look at the symmetries, it is about the synchronous variation of circle and dipole wave over the diameter or length of the dipole. In the electromagnetic interaction, the field orientation must also be maintained, because this is inherited from the primitive osci. Provided that the dipole wave changes synchronously, the variation problem can be limited to the circular waves! The diameter of the circle can therefore change not only over the reduced wavelength, but also over the number of windings, which in turn depends over the total energy on the reduced wavelength. Since the solution is found with the local energetic minimum of the total energy, it amounts to the target value search in relation to the reduced wavelength!

Computationally, the variation problem deals with the binding energies resulting from the interactions. The spreadsheet created for the pair of up- and down-osci must be varied accordingly. One osci remains primitive as an associated boson, while the geometry of the other osci, the searched elementary particle, is changed within the limits shown above. This must be done separately for each possible winding type, since it fundamentally changes the calculation of the electromagnetic binding energy. The solutions to the variation problem show how the space-time plane of the formerly primitive circular wave is curved by the leptons. This result is irritating only in the first moment. It is a consequence of the spatial structure in the TO - see SEPARATION OF ROOMS.

One more comment on the boson as a partner-osci. Within the variation problem, it represents the energy reserve that can be continuously exploited by varying its reduced wavelength. So the Higgs mechanism hides already in the variation problem. In this sense, the boson can be regarded as a gravitational partner of the elementary particle, even if it only exists in "statu nascendi", i.e. can only be observed in quantum processes.

The elementary particles result from the local minima of its total energy. Nevertheless, a small difference remains in the overall energy balance of the osci-pair. For neutrinos it is the kinetic energy - massless only at c! For the electron and muon it is the rotational energy - for more see MUON.

The solutions of the variation problem shows that the TO is an "all inclusive theory".

last modification 01.03.2019

go to side ◀ 0 1 2 3 4 5 6 7 8 9 ▶