2 PREVIEW AND TEST PROTON, NEUTRON
ENGLISH ▶
PREVIEW
The approach should be discarded if it is not possible to determine the up- and down-osci in such a way that proton and neutron result. This is not trivial, since mass defects occur with the shell model (classical QM). Thereby an arithmetic symmetry shows up. This is associated with a perturbation (±) corresponding to the mass of the electron.
chapter TEST PROTON, NEUTRON see below
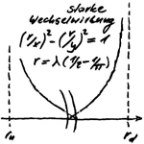
The up- and down-oscis build a shell model. With it the strong interaction can be disenchanted. Via the phenomenon of commutation, geometric symmetry is found. The strong interaction creates a special square-integratable probability space (L²). This is packed between the two known spaces, which result from the corresponding field theories. This refers to electromagnetic field theory and the general relativity (GR). A sandwich is formed, at whose transitions forget-functors act, which simplifies the theory enormously.
The arithmetic symmetry allows to generate a special continuum, the so-called e-continuum, for the pair of up- and down-osci. The principle of constriction leads to gravitational symmetry. If the arithmetic symmetry is abandoned, the other symmetries become continuous symmetries. The geometrical symmetry becomes the general symmetry with the symmetry energy as conserved quantity. The pair of up- and down-osci becomes the solution of a variation problem, in which it concerns pairs of primitive oszi. In this case, the Noether's theorem (NT) applies. In order to obtain the remaining elementary particles as oscis, the winding type of one of the oscis must be released. The question of how the variation of the oscis may look without violating the validity of the NT must therefore be clarified.
The following chapters discuss the solutions to the resulting variation problem. They are concerned with the existential proof of leptons (real quantum theory).
last modification 01.03.2019
TEST PROTON, NEUTRON
Only if the approach to the nucleons does not fail can the process continue. Until then, classical quantum mechanics will be the subject. Since protons and neutrons form a shell model of up- and down oscis, the following has to be tested:
- Are charge and spin correct? And if yes, is the shell model then unique?
- Can the reduced wavelengths for the up- and down-osci be determined in such a way that the masses of the proton and neutron are correct (the diameters are added).
Up- and down-osci are primitive oscis. Charge and spin thus result from the integration of E- and B-fields in the direction of propagation, according to the rules of school mathematics. The amplitude is set to ¼ so that the qunate numbers for charge and spin become 1. Spin 1 in the TO thus corresponds classically to ½. By definition, the value has something to do with the g-value (1 remains 1, instead of 2 times ½). At the dipole wave charge and spin result in 0. Behind the quantum number there is of course a vector in the TO, whose position in space is determined by symmetry. The quantum numbers of protons and neutrons are also determined by a vectorial intermediate calculation. The up- and down-oscis are nested according to the structural formulas for the proton and neutron respectively. The structure of the resulting shell model becomes unique only with the dilemma of QT.
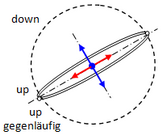
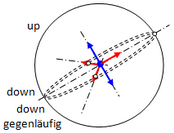
Attention, in the sketches you will only find the arrows that lift themselves away: blue = spin, red = charge.
proton: electric charge 1, spin 1.The circular orbit of the down osci is completely free.The circular orbits of the two up-osci lie in one plane and run in opposite directions.
neutron: electric charge 0, spin 1.The down oscis lie in one plane.The phase shift of the trajectories against each other is 120°.The up-osci can only rotate around its charge axis.
It is now a matter of determining the reduced wavelength λ of the up- and down-osci in such a way that the known masses of the proton and neutron result. Thus the result is known, but not the solution, which must be unambiguous in this case. This is reminiscent of school when, despite the known result, it was not at all clear what to do. A look at the schoolbook does not help if it is not clear where to look. Exactly this describes the situation. With the known structural formulas of neutron (1 up + 2 down) and proton (2 up + 1 down) it amounts to the solution of a linear system of equations. With the above shell model, however, mass defects occur, with which it is underdetermined. The β-decay is helpful in that it makes the division of the mass defects unambiguous. The computationally correct result results, however, only with adherence to the following symmetry:
md = ms + me und mu = ms - me, where ms is the mass of the arithmetic symmetry. Thus md - mu = 2me.
The index d stands for the down-osci, u for the up-osci and e for the electron. The actual calculation, which is not trivial, can be found in the PDF. It is important to understand that a clear solution was found via the known result. This requires the arithmetic symmetry, which is therefore part of the theory! In addition, only the mass of the electron is relevant as a perturbation, which is experimentally determined quite precisely.
Apart from the fact that the lower table is based on the upper table, the mass defects show that the neutron is more stable than the proton. The fact that the reality of this statement is not true is due to the disturbed impulse transmission of the proton: The up-shells can rotate freely in relation to the down-shell.
Excursus into the special relativity (SR): Since the TO includes the gravitational interaction, the Lorentz invariance of the primitive oszis should be detected. This is given when its transformations in the Minkowski space are elements of the actual Lorentz group SO(3,1). It is sufficient that the images of their geometry on themselves belong to the rotation group SO(3), which is obvious (mathematics for physicists).
last modification 24.02.2019