4 GRAVITATION UND NOETHER-THEOREM
GERMAN ▶
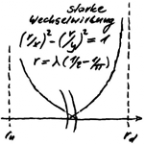
GRAVITATIVE WECHSELWIRKUNG
Die Idee zu seiner Berechnung ergibt sich mit der Gardine am Fenster. Werden mehrere Falten mittels einer Schlaufe gerafft, so führt deren Einschnürung zu einer Gegenreaktion, die mit der Gravitation gleichgesetzt werden kann (negativ). Die durch das Faltenband vordefinierten Falten der Gardine entsprechen der Skalierung des Gravitationsraumes. Dabei erinnert man sich, dass die Störung beim Paar aus Up- und Down-Oszi ± einer Elektronmasse betrug, womit die Skalierung des Gravitationsraumes gefunden ist - kurz e-Kontinuum genannt.Ausgehend vom Up- und Down-Oszi und deren Compton-Wellenlängeλu = 3,96741355771958 10-15 m and λd = 3,95448111261022 10-15 mdu = 1,66484999566855 10-15 m und dd = 1,65942313989184 10-15 m.
ergeben sich als Kreiswelle folgende DurchmesserDamit lässt sich der zu me passende Skalierungsfaktor w0 berechnen:w0 = ¼ (du - dd) = 1,35671394417761 10-18 mFür den 0-Radius ergibt sich damit
Die gravitative Symmetrie von Up-und Down-Oszi ist somit gefunden.
Mit der gravitativen Symmetrie ist die zunächst aufgrund des β-Zerfalls bestimmte arithmetische Symmetriemasse korrekt, was zu beweisen war! Gravitation wird also durch das Prinzip der Einschnürung im Raum-Zeit-Kontinuums erzeugt. Als solches besitzt es allgemeine Gültigkeit. Achtung, das Fehlen einer Spin-Komponente in den Einsteinschen Feldgleichungen ist mit der TO kein Fehler, sondern ein Muss! Ausgehend vom Paar aus Up- und Down-Oszi läst sich die gravitative Symmetrie verallgemeinern. Für ein Paar von Oszis, das der allgemeinen Symmetrie genügt, gilt dann
Eges/w = r0 = r1 + r2, wobei r1 = E2/w und r2 = E1/w ist.
Diese Symmetrie zeigen Kreis- wie Dipolwellen! In Bezug auf das sich ergebende Variationsproblem bedeutet dies, dass die Energiedichte eine lokale Größe ist. Den Weg, zu der einen universell gültigen Energiedichte des Quantenvakuums, zeigt später die Aufwärtsoszillation des Neutrino-Oszis.
letzte Änderung 24.02.2019
VERALLGEMEINERUNG UND NOETHER-THEOREM
Das Noether-Theorem (kurz NT) besagt, dass jede kontinuierliche Symmetrie zu einer Erhaltungsgröße führt, wobei die Symmetrie äquivalent zur „Invarianz unter einer Operation" ist. Dies ist seine allgemeingültigste Formulierung. Wenn sie nicht passt, passt keine. In diesem Fall müsste das NT gleich für alle drei Wechselwirkungen gelten, und zwar bei einer gemeinsamen Erhaltungsgröße.
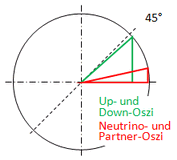Der oben verwendete Konjunktiv kann für Paare primitiver Oszis, die der geomerischen Symmetrie genügen, entfallen. Das Paar aus Up- und Down-Oszi ist die einzige Lösung des zugehörigen Variationsproblems. Die ist sofort zu erkennen, wenn alle Beziehungen, die sich aus den bislang erkannten Symmetrien ergeben, in einem Tabellenblatt zusammengestellt werden. Zur arithmetischen Symmetrie, also der Störung um plus/minus einer Elektronenmasse, kommt es natürlich nur beim Paar aus Up- und Down-Oszi, der Lösung. Mit der geometrischen Symmetrie, die fortan allgemeine Symmetrie heißen soll, gilt der Satz des Pythagoras. Wird die Symmetrieenergie auf 1 normiert, so ist dies im Einheitskreis darstellbar. Die Symmetrieenergie bzw. der Radius 1 ist die Erhaltungsgröße im NT. Das Variationsprobem soll nun so weit verallgemeiner werden, dass die Lösungen die Leptonen einschließen. Dazu wird die Wicklungsart eines der Oszis freigegeben. Damit das Variationsproblem lösbar bleibt, darf es sich nur auf eine bestimmte Wicklungsart beziehen. Trotz dieser Fallunterscheidung, ergeben sich damit mehr Möglichkeiten der geometrische Variation als im Fall des primitiven Oszis. Die Möglichkeiten sind soweit einzuschränken, dass das NT gültig bleibt. Dies setzt voraus, dass die Symmetrien weiter gelten. Da, wo dies nicht direkt ersichtlich ist, kann auf die „Invarianz unter der entsprechenden Operation", also unter der entsprechenden Wechselwirkung zurückgegriffen werden.
Schaut man sich die Symmetrien daraufhin an, so geht es um die synchrone Variation von Kreis und Dipolwelle über den Durchmesser bzw. über die Länge des Dipols. Bei der elektromagnetischen WW ist zudem die Feldorientierung beizubehalten, denn die wird vom primitiven Oszi vererbt. Die synchrone Änderung der Dipolwelle vorausgesetzt, kann das Variationsproblem auf die Kreiswellen beschränkt werden! Der Kreisdurchmesser kann sich damit nicht nur über die reduzierte Wellenlänge, sondern auch über die Wicklungszahl ändern, wobei die aber wieder über die Gesamtenergie von der reduzierte Wellenlänge abhängt. Da die Lösung mit dem lokalen energetische Minimum der Gesamtenrgie gefunden ist, läuft es auf die Zielwertsuche in Bezug auf die reduzierte Wellenlänge hinaus!
Rechnerisch geht es im Variationsproblem um die Bindungsenergien, die sich aufgrund der Wechselwirkungen ergeben. Dass, für das Paar aus Up- und Down-Oszi erstellte Tabellenblatt, ist entsprechend zu variieren. Ein Oszi bleibt als zugehöriges Boson primitiv, während die Geometrie des anderen Oszi, dem gesuchten Elementarteilen, in den oben aufgezeigten Grenzen verändert wird. Dies muss für jede mögliche Wicklungsart getrennt geschehen, da sich die Berechnung der elektromagnetischen Bindungsenergie durch sie grundlegend ändert. Die Lösungen des Variationsproblems zeigen, wie die Raumzeitebene der vormals primitiven Kreiswelle durch die Leptonen gekrümmt wird. Dies Ergebnis ist nur im ersten Moment irritierend. Es ist eine Folge der Raumstruktur in der TO - siehe SEPARATION DER RÄUME.
Noch eine Anmerkung zum Boson als Partner-Oszi. Es stellt innerhalb des Variationsproblems die Energiereserve dar, die über die Variation seiner reduzierten Wellenlänge stufenlos ausgeschöpft werden kann. Der Higgs-Mechanismus steckt also bereits im Variationsproblem. In diesem Sinne kann das Boson als gravitativer Partner des Elementarteilchens angesehen werden, auch wenn es nur in „statu nascendi“ existiert, also nur bei Quantenprozessen zu beobachten ist.
Die Elementarteilchen ergeben sich über die lokalen Minima seiner Gesamtenergie. In Bezug auf die gesamte Energiebilanz des Oszi-Paares bleibt jedoch eine kleine Differenz. Bei den Neutrinos ist es die kinetische Energie - masselos erst bei c! Beim Elektron und Myon ist es die Rotationsenergie - mehr siehe MYON.
Die Lösungen des Variationsproblems zeigen, dass die TO eine Theorie des „all inclusive“ ist.
letzte Änderung 01.03.2019