6 ELECTRON, MYON AND TAUON AS OSCIS
ENGLISH ▶
The elementary particles must result as a solution to the variation problem. This refers to a pair of oscis that satisfies the general symmetry, where the symmetry energy is known as the conserved quantity. The solutions are where the energy of the elementary particle has a local minimum summed over all binding energies. This problem can be solved computationally, because besides the general symmetries other symmetries and exchange rules apply. If the calculation of the total energy of the found pair does not add up, it has to be clarified which energy form(s) are in the rest.
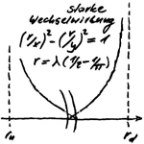
Due to the quantum numbers, the winding type in the electron can only be counter-rotating: Charge ±1, Spin 1 (classic ½). Circle wave thus builds double helix with turning points, which turn out to be loops. The double helix could be wrongly regarded as collapsed with respect to the strong interaction (integration interval 0). However, since only the projection in the plane of the E-field is relevant (forget-functor), this is not the case. The strong alternating winding therefore wants to wind up the double helix further.
The Coulomb forces also have the same effect, since the charge differences between the windings become smaller with increasing number of turns. Based on packing density of windings, this effect of double helix has priority over radial repulsion forces. Since an equilibrium has to be established as the radius becomes smaller, also the calculation method has been found.
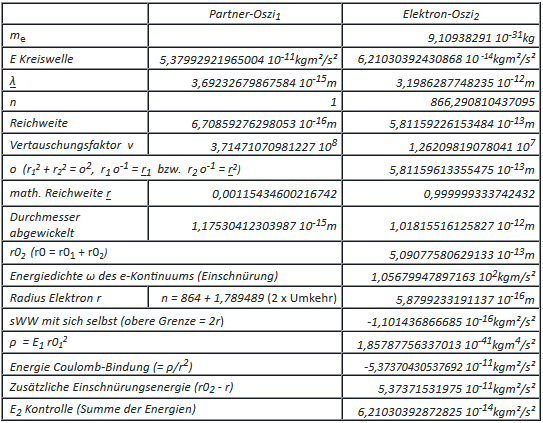
The variation problem should have three solutions. Two were found directly: Electron and muon. Even if the associated boson is destroyed energetically, there is still a rest, which is only obvious with the muon. With the electron, he's hiding in the arithmetic inaccuracy. It is the rotational energy resulting from dynamic balancing of the reversal loops. The loops are the cause of the magnetic anomaly!
The electron shows a special feature in the TO. This consists in the fact that its energy remains unchanged with the transformation from primitive osci to electron-osci. This allows tunneling through the strong interaction of its circular wave, which is still present in the primitive osci. Thus, instantaneously, the range of the strong interaction is bridged, which is known as tunnel effect. When wound up, this will demand overcoming the diameter of the circle, which however is only possible along the circumference of the circle. With this half round of penalties, it all adds up to c again. Based on the values in the table above, the resolution of a scanning tunneling microscope can be predicted. After that, the effect is only likely to start below a barrier width b ≤ 2r02 + r2 and become maximum at b ≤ 2r02:
2r02 + r2 = 1,59931… 10-12 m ≈ 1600 fm = 1,6 pm, and2r02 = 1,01815… 10-12 m ≈ 1018 fm =1,018 pm, which matches the vertical resolution!
Higgs particle and e-boson (Boson of the electron): If one calculates the mass defect of the e-boson due to the constriction in the space-time continuum, one arrives at the mass of the H-boson = 2,25241710053953 10-25 kg by halving it. Charge and spin of the e-boson are 1, of the H-boson 0. Charge and spin can be cancelled by identical but counter-rotating waves, which requires at least two e-bosons. In this case, the circular waves form an osci-eight. Even if the quantum numbers are now arithmetically correct, the geometric result is a dipole moment. The solution is 4 e-bosons arranged in a square by rotating the circular wave alternately to the right and to the left, thus cancelling the dipole moments of the individual combination of two. Relative, the extent of constriction remains the same: doubling at twice the size of the structure. The mass defect is true now. The generation and decay channels of the H-boson support this idea!
Weiter mit dem Myon als Oszi:
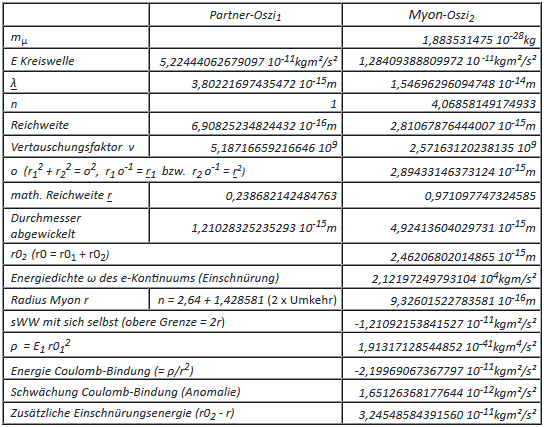
In contrast to the electron, the rotational energy is of importance here. Behind this is the dynamic balancing of the reversal loops, which is ultimately reflected in the spin resonance frequency. This is known and should now be recalculated. The single osci is mounted as a gyroscope without forces, so nutation can be excluded (kinetics). With a suitable rotation frequency, precession no longer occurs! Deciding is that the resulting spin must then be 1.The orthogonal torque ED = 8,36174112640316 10-12 kgm²/s² can be calculated from the energy of the Coulomb bond and its component weakened in the direction of the axis of rotation (Pythagoras). ED stands for electromagnetic anomaly. Except for the sign, this must correspond to the moment resulting from the unbalance of the mass defect, where ED = MD.
With Sμ = 1,93794205529255 1022 s-1 as frequency of the circular wave
then Iμ = ED/Sμ = 4,31475291202186 10-34 kgm²/s is the tilting pulse.
The frequency of the circular wave can be written as a product:
Sμ = Rμ SRμ, where Rμ is the rotation frequency and SRμ is the spin resonance frequency.
For the rotation frequency ω = 2π Rμ, applies, and thus MD = kD lμ rμ (2π Rμ)².
If kD were known, the rotation frequency, and thus also the resonance frequency, could now be determined. Since this is not the case, the reverse is the case. With the value for the resonance frequency from the literature kD is calculated, in the hope that the value reveals how kD can also be calculated in other ways.
With SRμ= 1,3554 108 s-1 the result for Rμ = 1,42979345971119 1014 s-1, and thus for
kD = 1,8904891686749 10-11 kg, where kD c² = 1,69908693069243 106 kgm²/c² ≈ 1,06 1016 GeV.
SUSY says hello. The above value indicates the assumed maximum interaction energy. This also includes gravitational interaction. It can therefore be assumed that the space-time continuum ruptures at this energy. The double helix of the electron is now to be observed in the appropriate vector field, a Jacobian field. In it, the propagation line of the circular wave is to be regarded as the limit curve of causal geodesists. With the reversal loops, their geometry has no conjugated points. Since this is the singularity theorem after "Hawking and Penrose" is fulfilled, applies:
The reversal loops form the smallest possible holes in the space-time continuum!
Exkurs Entropie: It can only increase if it is not constant. In the empty universe without zero fluctuation - as in the TO - entropy is constant, and potential energy assumes its minimum, assuming that the energy is positive. If it is negative, as here, its absolute amount must remain constant. Entropy and prestressing are therefore related. The connection is described by the basic equation of the GR by connecting G-Term and Λ-Term. G must now be replaced by the gravitational constant G00 of the empty universe (see chapter NEUTRIONOS ...). After the paragraph to "SUSY", the reversal loops of the leptons tear holes into the space-time continuum with a defined mass defect kD (dimension kg). In the prestressed space-time continuum, kD stands for the hardness of the continuum. The following equation can be established by simply considering the dimensions.
With w00= E00/r = -6,47013541836098 10-11 kgm/s² and G00 = -6,47013541836098 10-11 m³/kgs²,then G00 kD Ʌ = w00/kD = -3,4224662725235800 m/s², where Ʌ = 2,79802514510710 1021 m-2 ist.
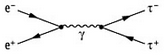Continue with the tauon as osci. It is the third and heaviest lepton with charge = ±1 and spin = 1 in the TO. The fact that it does not result from the method that was successful with the electron and muon must be directly related to its creation. It is always created together with its antiparticle!
With the tauon, the E-field cannot lie in the circular plane as before, because then the wavelength is too short to maintain the minimum radius of curvature. The only solution that does not violate any of the conditions is the entangled eight - see right. As with the electron and muon, there is an electromagnetic anomaly that is far greater than that of the muon (dynamic balancing). The quantum number of the charge is thus smaller than 1. Its increase to 1 requires a torsional moment ED as with the muon (further as with the muon).It is now about the validity of the CPT theorem in the TO. Its violation would contradict the Lorentz invariance and thus the special relativity theory. The subject is obvious at this point, as the tauon has a rather unusual design. With the model of the Tauon circular wave it becomes clear that not only the propagation line but also the field orientations have to be considered. Starting from the primitive Oszi, there is an obvious arrangement of the coordinate system. The folding dipole as rotation axis defines the z-axis and the plane of the E-field, in which the circular wave lies, forms the xy-plane.
The P in CPT stands for space reflection (parity transformation). This is identical to the mirroring at the xy plane, followed by a 180° rotation of the xy plane around the z axis. At the geometry of the circular wave of the tauon it becomes plausible that the reflection leads to an exchange of the half waves, which cannot be reversed with any rotation. The substitution can only be abolished with a phase shift around π. In the case of -π this can be understood as a time reversal, whereby it does not have to exist in reality (sine as a periodic function). There is no time reversal in the TO, since entropy does not disappear even in the quantum vacuum (see Entropy Excursus above).
PT invariance is given with the last paragraph. The C parity is equivalent to a charge conjunction, i.e. again a phase shift around π. The charge in the oscillator results from integration via the wave. According to their rules, the result does not change unless the leptons (charge ±1) are involved, which is due to their special winding type. C-parity and time reversal cancel each other out in their effect, since 2π corresponds to one wavelength. The CPT transformation thus becomes the P transformation, which shows the validity of the CPT theorem for the TO.
last modification 29.03.2019