ELEKTRON, MYON UND TAUON ALS OSZIS
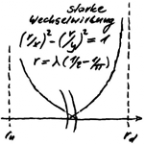
Die Elementarteilchen müssen sich als Lösung des Variationsproblems ergeben. Das bezieht sich auf ein Paar von Oszis, die der allgemeinen Symmetrie genügt, wobei die Symmetrieenergie als Erhaltungsgröße bekannt ist. Die Lösungen liegen dort, wo die Energie des Elementarteilchens über alle Bindungsenergien ein lokales Minimum aufweist. Dies Problem ist rechnerisch lösbar, da neben der allgemeinen Symmetrien weitere Symmetrien und Vertauschungsregeln gelten. Geht die Rechnung bezüglich der Gesamtenergie des gefundenen Paares nicht auf, so ist zu klären, welche Energieform(en) im Rest stecken. Aufgrund der Quantenzahlen kann die Wicklungsart im Elektron nur gegenläufig sein: Ladung ±1, Spin 1 (klassisch ½). Die Kreiswelle bildet damit eine Doppelhelix mit Umkehrpunkten, die sich als Schlaufen entpuppen. Die Doppelhelix könnte in Bezug auf die starke WW fälschlich als zusammengefallen angesehen werden (Integrationsintervall 0). Da aber nur die Projektion in der Ebene des E-Feldes relevant ist (Vergißfunktor), ist dies nicht so. Die starke WW will daher die Doppelhelix weiter aufwickeln. Den gleichen Effekt haben auch die Coulombkräfte, denn mit zunehmender Windungszahl werden die Ladungsdifferenzen zwischen den Windungen kleiner. Aufgrund der Packdichte der Windungen hat dieser Effekt der Doppelhelix Vorrang vor den radialen Abstoßungskräften. Da sich mit kleiner werdendem Radius ein Gleichgewicht einstellen muss, ist auch die Berechnungsmethode gefunden.
Das Variationsproblem müsste drei Lösungen besitzen. Zwei wurden direkt gefunden: Elektron und Myon. Auch wenn das zugehörige Boson energetisch vernichtet wird, bleibt noch ein Rest, der aber erst beim Myon auffällt. Beim Elektron geht er in der Rechenungenauigkeit unter. Es ist die Rotationsenergie, die sich durch dynamisches Auswuchten der Umkehrschlaufen ergibt. Die Schlaufen sind die Ursache der magnetischen Anomalie!
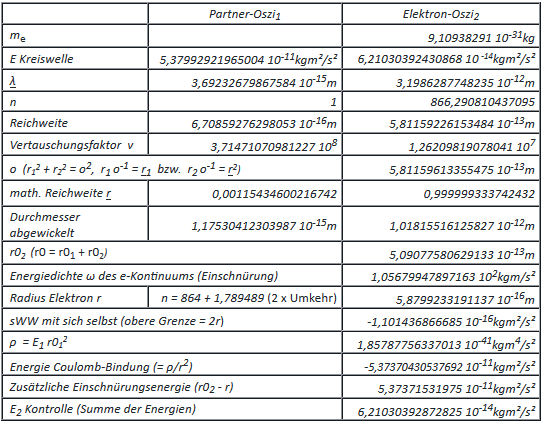
Das Elektron zeigt in der TO eine Besonderheit. Die besteht darin, dass seine Energie mit der Transformation vom primitiven Oszi zum Elektron-Oszi unverändert bleibt. Dies erlaubt das Tunneln, und zwar über die starke WW seiner Kreiswelle, die beim primitiven Oszi noch vorhanden ist. Damit wird instantan, die Reichweite der starken WW überbrückt, was als Tunneleffekt bekannt ist. Andererseits erfordert dies mit dem Abwickeln die Überwindung des Kreisdurchmessers, was aber nur entlang des Kreisumfangs möglich ist. Mit dieser halben Strafrunde läuft es insgesamt wieder auf c hinaus. Aufgrund der Werte in obiger Tabelle lässt sich die Auflösung eines Rastertunnelmikroskops vorhersagen. Danach dürfte der Effekt erst unterhalb einer Barrierebreite b ≤ 2r02 + r2 einsetzen und bei b ≤ 2r02 maximal werden:
2r02 + r2 = 1,59931… 10-12 m ≈ 1600 fm = 1,6 pm, und2r02 = 1,01815… 10-12 m ≈ 1018 fm =1,018 pm, was zur vertikalen Auflösung passt!
Higgs-Teilchen und e-Boson (Boson des Elektrons). Rechnet man den Massendefekt des e-Bosons aufgrund der Einschnürung im Raum-Zeit-Kontinuum aus, so kommt man durch Halbierung auf die Masse des H-Bosons = 2,25241710053953 10-25 kg. Ladung und Spin des e-Bosons sind 1, des H-Bosons aber 0. Ladung und Spin lassen sich über identische, aber gegenläufig drehende Wellen annullieren, womit mindestens zwei e-Bosonen benötigt werden. In diesem Fall bilden die Kreiswellen eine Oszi-Acht. Auch wenn die Quantenzahlen jetzt arithmetisch stimmen, ergibt sich aber geometrisch ein Dipolmoment. Die Lösung sind 4 e-Bosonen, die im Rechteck angeordnet sind, indem die Kreiswelle abwechseln rechts und linksherum drehen, womit sich die Dipolmomente der einzelnen Zweierkombination aufheben. Da das Ausmaß der Einschnürung trotz doppelter Größe der Struktur gleich bleibt, stimmt jetzt auch der Massendefekt. Die Erzeugungs- und Zerfallskanäle vom H-Boson stützen diese Vorstellung!
Weiter mit dem Myon als Oszi:
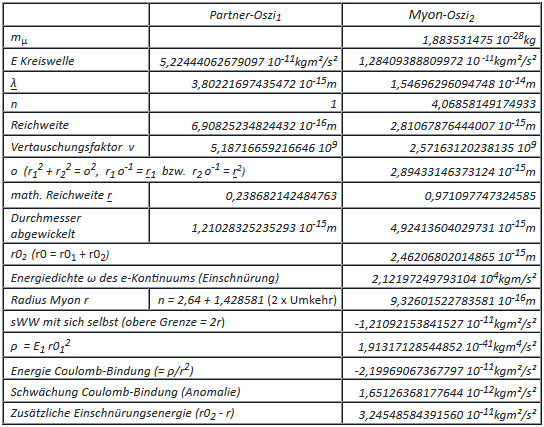
 Die Rotationsenergie fällt hier im Gegensatz zum Elektron ins Gewicht. Dahinter verbirgt sich das dynamische Auswuchten der Umkehrschlaufen, das sich letztlich in der Spin-Resonanzfrequenz zeigt. Die ist bekannt und soll nun nachgerechnet werden. Der einzelne ungeundene Oszi-Kreisel ist im Raum prinzipiell kräftefrei gelagert. Es tritt also weder Nutation noch Präzession auf. Entscheiden ist, dass der Betrag des resultierenden Spins 1 ergeben muss! Aus der Energie der Coulombbindung und seiner in Richtung der Drehachse geschwächten Komponente lässt sich das dazu orthogonale Drehmoment ED = 8,36174112640316 10-12 kgm²/s² berechnen (Pythagoras). ED steht für die elektromagnetische Anomalie. Die muss bis auf das Vorzeichen dem Moment entsprechen, das sich aus der Unwucht des Massendefektes ergibt, womit ED = MD ist.
Die Rotationsenergie fällt hier im Gegensatz zum Elektron ins Gewicht. Dahinter verbirgt sich das dynamische Auswuchten der Umkehrschlaufen, das sich letztlich in der Spin-Resonanzfrequenz zeigt. Die ist bekannt und soll nun nachgerechnet werden. Der einzelne ungeundene Oszi-Kreisel ist im Raum prinzipiell kräftefrei gelagert. Es tritt also weder Nutation noch Präzession auf. Entscheiden ist, dass der Betrag des resultierenden Spins 1 ergeben muss! Aus der Energie der Coulombbindung und seiner in Richtung der Drehachse geschwächten Komponente lässt sich das dazu orthogonale Drehmoment ED = 8,36174112640316 10-12 kgm²/s² berechnen (Pythagoras). ED steht für die elektromagnetische Anomalie. Die muss bis auf das Vorzeichen dem Moment entsprechen, das sich aus der Unwucht des Massendefektes ergibt, womit ED = MD ist.Mit Sμ = 1,93794205529255 1022 s-1 als Frequenz der Kreiswelle
ist dann Iμ = ED/Sμ = 4,31475291202186 10-34 kgm²/s der Kippimpuls.
Die Frequenz der Kreiswelle lässt sich als Produkt schreiben:
Sμ = Rμ SRμ, wobei Rμ die Rotationsfrequenz und SRμ die Spin-Resonanz-Frequenz ist.
Für die Rotationsfrequenz gilt ω = 2π Rμ, und damit ist MD = kD lμ rμ (2π Rμ)².
Wäre kD bekannt, so ließe sich jetzt die Rotationsfrequenz, und damit auch die Resonanzfrequenz bestimmen. Da dies nicht so ist, wird umgekehrt vorgegangen. Mit dem Wert für die Resonanzfrequenz aus der Literatur wird kD berechnet, und zwar in der Hoffnung, dass der Wert verrät, wie sich kD auch auf anderem Wege berechnen lässt.
Mit SRμ= 1,3554 108 s-1 ergibt sich für Rμ = 1,42979345971119 1014 s-1, und damit für
kD = 1,8904891686749 10-11 kg, womit kD c² = 1,69908693069243 106 kgm²/c² ≈ 1,06 1016 GeV ist.
SUSY lässt grüßen. Bei obigem Wert liegt die vermutete maximale Wechselwirkungsenergie. Dazu gehört auch die gravitative WW. Also kann davon auszugehen werden, dass bei dieser Energie das Raumzeitkontinuum aufreißt. Dazu betrachte man die Einschnürung im passenden Vektorfeld, einem Jacobifeld. In ihm ist die Ausbreitungslinie der Kreiswelle als Grenzkurve kausaler Geodäten anzusehen. Die weist, obwohl die Doppelhelix, von den Umkehrschlaufen einmal abgesehen, dicht liegt, keine konjugierten Punkte auf. Da damit das Singularitätstheorem nach Hawking und Penrose erfüllt ist, gilt:
Die Umkehrschlaufen bilden die kleinsten möglichen Löcher im Raum-Zeit-Kontinuum!
Mit w00= E00/r = -6,47013541836098 10-11 kgm/s² und G00 = -6,47013541836098 10-11 m³/kgs²,ist G00 kD Ʌ = w00/kD = -3,4224662725235800 m/s², womit Ʌ = 2,79802514510710 1021 m-2 ist.
 Weiter mit dem Tauon als Oszi. Es ist das dritte und schwerste Lepton mit Ladung = ±1 und Spin = 1 in der TO. Dass es sich mit der Methode, die beim Elektron und Myon erfolgreich war, nicht ergibt, muss in direktem Zusammenhang zu seiner Entstehung stehen. Es entsteht immer zusammen mit seinem Antiteilchen!
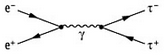
Weiter mit dem Tauon als Oszi. Es ist das dritte und schwerste Lepton mit Ladung = ±1 und Spin = 1 in der TO. Dass es sich mit der Methode, die beim Elektron und Myon erfolgreich war, nicht ergibt, muss in direktem Zusammenhang zu seiner Entstehung stehen. Es entsteht immer zusammen mit seinem Antiteilchen! Zudem kann das E-Feld nicht wie bislang in der Kreisebene liegen, denn dann ist die Wellenlänge zu kurz um den minimalen Krümmungsradius einzuhalten. Die einzige Lösung, die keine der einzuhaltenden Bedingungen verletzt, ist die verschränkte Acht - siehe rechts. Es liegt also wie beim Elektron und Myon eine elektromagnetische Anomalie vor, die noch weitaus größer als beim Myon ausfällt (Thema dynamisches Auswuchten). Die Quantenzahl der Ladung ist so vom Betrag kleiner 1. Seine Anhebung auf 1 erfordert wie beim Myon ein Drehmoment ED
Zudem kann das E-Feld nicht wie bislang in der Kreisebene liegen, denn dann ist die Wellenlänge zu kurz um den minimalen Krümmungsradius einzuhalten. Die einzige Lösung, die keine der einzuhaltenden Bedingungen verletzt, ist die verschränkte Acht - siehe rechts. Es liegt also wie beim Elektron und Myon eine elektromagnetische Anomalie vor, die noch weitaus größer als beim Myon ausfällt (Thema dynamisches Auswuchten). Die Quantenzahl der Ladung ist so vom Betrag kleiner 1. Seine Anhebung auf 1 erfordert wie beim Myon ein Drehmoment ED (weiter wie beim Myon).
Es soll nun um die Gültigkeit des CPT-Theorems in der TO gehen. Seine Verletzung würde zum Widerspruch zur Lorentzinvarianz und damit zur speziellen Relativitätstheorie stehen. Das Thema liegt an dieser Stelle nahe, da das Tauon eine recht ungewöhnliche Form aufweist. Mit dem Modell der Tauon-Kreiswelle wird deutlich, dass neben der Ausbreitungslinie auch die Feldorientierungen zu beachten sind. Ausgehend vom primitiven Oszi gibt es eine naheliegende Anordnung des Koordinatensystems. Der Faltdipol als Drehachse legt die z-Achse fest und die Ebene des E-Feldes, in der die Kreiswelle liegt, bildet die xy-Ebene.
PT-Invarianz ist mit dem letzten Absatz gegeben. Die C-Parität kommt einer Ladungskonjunktion gleich, also wieder einer Phasenverschiebung um π. Die Ladung im Oszi ergibt sich durch Integration. Nach deren Regeln ändert sich das Ergebnis nicht, es sei denn, es handelt sich um die Leptonen (Ladung ±1), was an den ihrer speziellen Wicklungsart liegt. C-Parität und Zeitumkehr heben sich so in ihrer Wirkung auf, da 2π einer Wellenlänge entspricht. Aus der CPT-Transformation wird somit die P-Transformation, womit die Gültigkeit des CPT-Theorems für die TO gezeigt ist.
letzte Änderung 24.02.2019